Extensão do conceito de cilindro

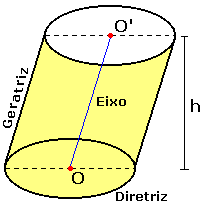
As características apresentadas antes para cilindros circulares, são também 
possíveis para outros tipos de curvas diretrizes, como: elipse, parábola, 
hipérbole, seno ou outra curva simples e suave num plano.

Mesmo que a diretriz não seja uma curva conhecida, ainda assim existem cilindros obtidos quando a curva diretriz é formada por uma reunião de curvas simples. Por exemplo, se a diretriz é uma curva retangular, temos uma situação patológica e o cilindro recebe o nome especial de prisma.

Em função da curva diretriz, o cilindro terá o nome de cilindro: elíptico, parabólico, hiperbólico, sinuzoidal (telha de eternit).

Classificação  dos  cilindros circulares

1. Cilindro circular oblíquo: Apresenta as geratrizes oblíquas em relação aos planos das bases.
2. Cilindro circular reto: As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo.
3. Cilindro eqüilátero: É um cilindro de revolução cuja seção meridiana é um quadrado.